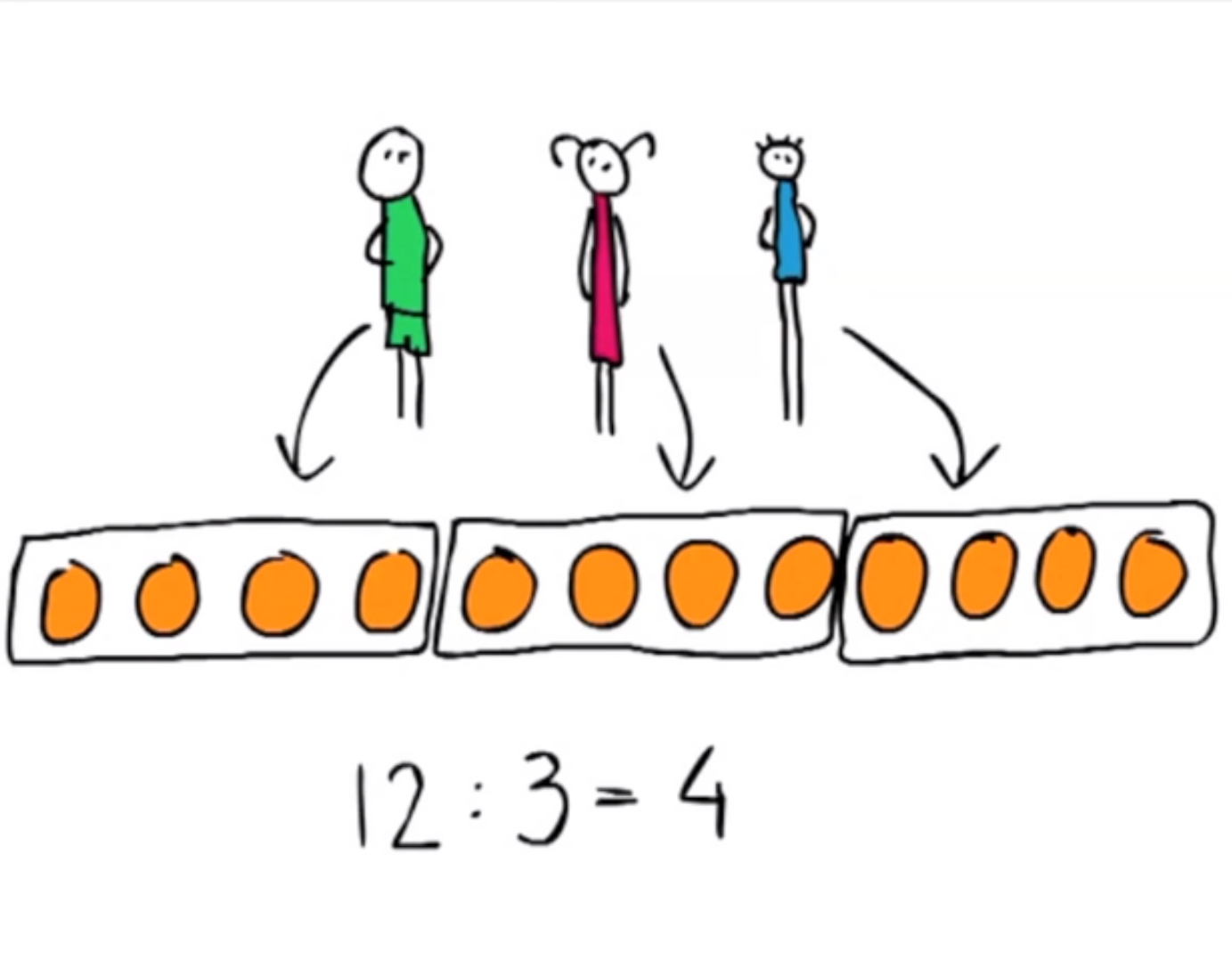
1 – Wat is delen? Uitleg over de betekenis van delen. Voorbeelden waarbij een aantal voorwerpen verdeeld wordt onder een aantal kinderen. Uitleg filmpje Werkbladen met antwoordbladen
	2 – Delen en vermenigvuldigen horen bij elkaar Uitleg over het feit dat delen de omgekeerde bewerking is van vermenigvuldigen. Dit geeft ook de mogelijkheid om de uitkomst van een deling te controleren met een vermenigvuldiging. Uitleg filmpje Werkbladen met antwoordbladen
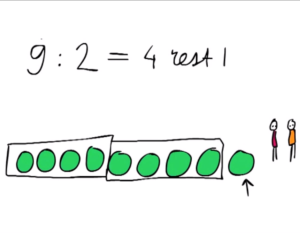	3 – Delen met rest Als je bijvoorbeeld 9 aardbeien wilt verdelen onder twee kinderen, blijft er één aardbei over. Die ene aardbei is ‘de rest’ die overblijft na de verdeling. Uitleg filmpje Werkbladen met antwoordbladen
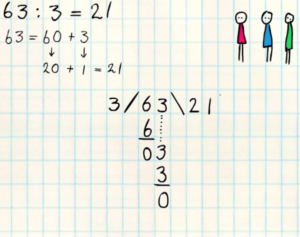	4 – Een staartdeling maken Hier worden een aantal zeer eenvoudige staartdelingen voorgedaan. Door de eenvoudig gekozen getallen wordt het duidelijk waarom zo’n staartdeling tot het goede antwoord leidt en waarom een staartdeling de handigste manier is voor het oplossen van een deelsom. Uitleg filmpje Werkbladen met uitgewerkte antwoordbladen
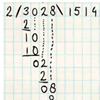	5 – Eenvoudige staartdeling zonder rest Hier worden nog een paar eenvoudige staartdelingen voorgedaan, nu wel met af en toe een ’tussen-rest’. Door de eenvoudig gekozen getallen wordt nogmaals duidelijk waarom zo’n staartdeling tot het goede antwoord leidt en waarom een staartdeling de handigste manier is voor het oplossen van een deelsom. Uitleg filmpje Werkbladen met uitgewerkte antwoordbladen
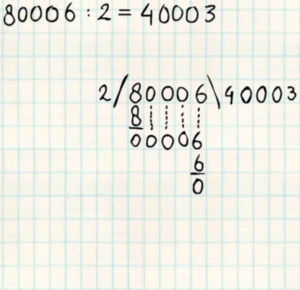	6 – Staartdeling met nullen in het antwoord Het aanhalen van nullen lijkt in het begin moeilijk maar is in feite zeer eenvoudig. Door de uitleg blijkt ook nu heel duidelijk waarom de staartdeling altijd snel en effectief tot het goede antwoord leidt. Uitleg filmpje Werkbladen met uitgewerkte antwoordbladen Uitleg filmpje staartdeling: 612 : 3 Uitleg filmpje staartdeling: 39500 : 5 Uitleg filmpje staartdeling: 6609 : 3
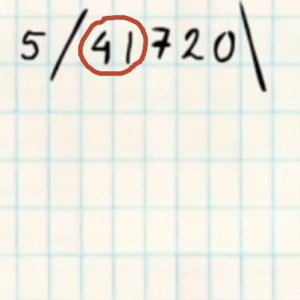	7 – Iets moeilijker staartdeling Soms moet je bij het begin van een staartdeling niet alleen naar het eerste cijfer van het deelgetal kijken maar naar de eerste twee cijfers. Dit is heel begrijpelijk maar het is even wennen in het begin. Na een paar keer oefenen is ook dit soort staartdeling heel eenvoudig zelf te maken. Uitleg filmpje Werkbladen met uitgewerkte antwoordbladen Uitleg filmpje staartdeling: 147 : 7
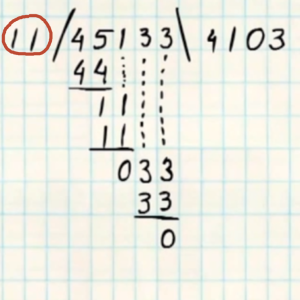	8 – Staartdeling met deler groter dan 10 Als de deler groter is dan tien, gaat de staartdeling in feite toch op precies dezelfde manier. Het is alleen even wennen en een paar keer goed oefenen. Uitleg filmpje Werkbladen met uitgewerkte antwoordbladen Uitleg filmpje staartdeling: 144 : 12 Uitleg filmpje staartdeling: 2623 : 43
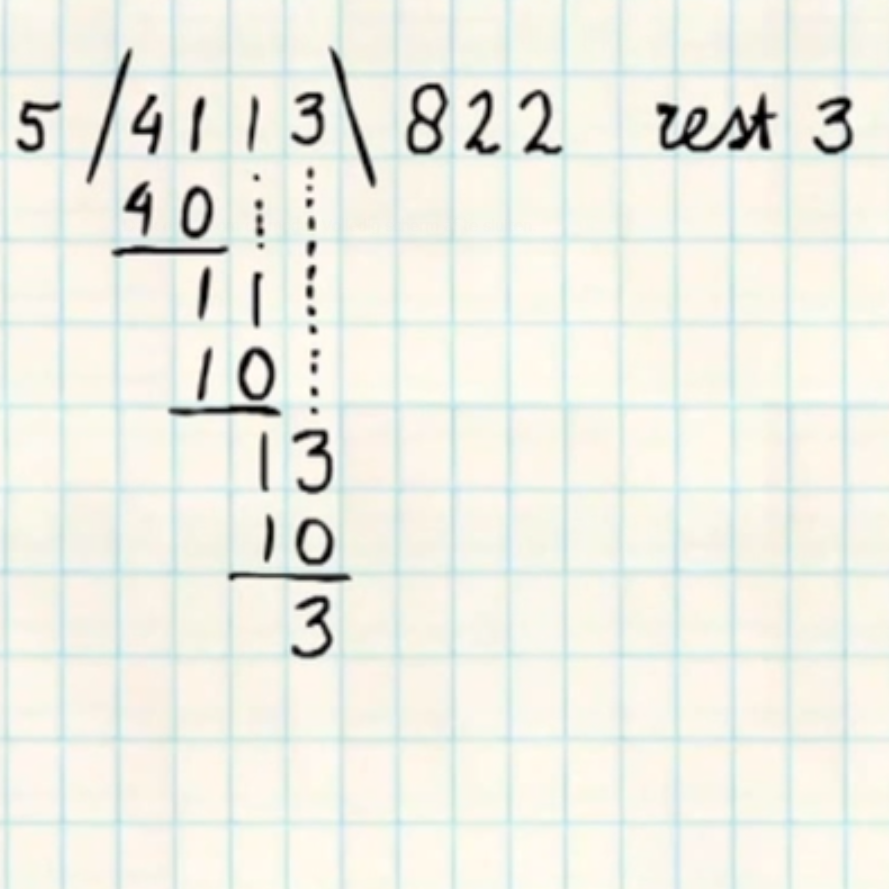	9 – Staartdeling met rest Soms staat er aan het eind van een staartdeling geen nul maar een groter getal. Dit getal noemen we de ‘rest’. In het eerste filmpje is al uitgelegd dan er soms iets over blijft als je bijvoorbeeld een aantal aardbeien onder een aantal kinderen verdeelt. De staartdeling wordt er niet moeilijker door. Uitleg filmpje Werkbladen met uitgewerkte antwoordbladen Uitleg filmpje staartdeling: 815 : 3 Uitleg filmpje staartdeling: 8923 : 7

De hapmehode versus de staartdeling.

De hapmethode is gebaseerd op het feit dat je delen kunt zien als herhaald aftrekken.
De staartdeling is gebaseerd op het feit dat je delen kunt zien als het omgekeerde van vermenigvuldigen.

Zoals aftrekken de omgekeerde bewerking is van optellen, zo is delen de omgekeerde bewerking van vermenigvuldigen.

Voor kinderen is het na een paar keer uitleggen duidelijk dat:
8 : 4 = 2 omdat 2 x 4 = 8
Ze weten immers ook al dat:
7 – 3 = 4 omdat 4 + 3 = 7

Het noodzakelijke inzicht dat delen de omgekeerde bewerking is van vermenigvuldigen, leidt tot de veel eenvoudiger te leren staartdeling. Ook zwakke rekenaars kunnen de staartdeling goed begrijpen en onder de knie krijgen.

De staartdeling heeft daarbij ook het voordeel dat het tot een beter getalinzicht leidt:

• Delen is de omgekeerde bewerking van vermenigvuldigen en aftrekken is de omgekeerde bewerking van optellen.
• Met de staartdeling is het direct duidelijk dat je het antwoord van een som kunt controleren via een vermenigvuldiging.
• Met de staartdeling wordt later het verband tussen de ‘rest’ van een deelsom en een kommagetal of breuk vanzelfsprekend en eenvoudig.
• Met de staartdeling kun je rechtstreeks uitrekenen en begrijpen dat
  1/4 = 0,25 en 1/3 = 0,333333…  enz.

Hier onder de video’s die horen bij de paragrafen over het delen met hele getallen.
Deze video’s staan ook op de pagina die hoort bij een paragraaf. Ga voor oefenen (online of met werkbladen) naar de paragraaf-pagina.