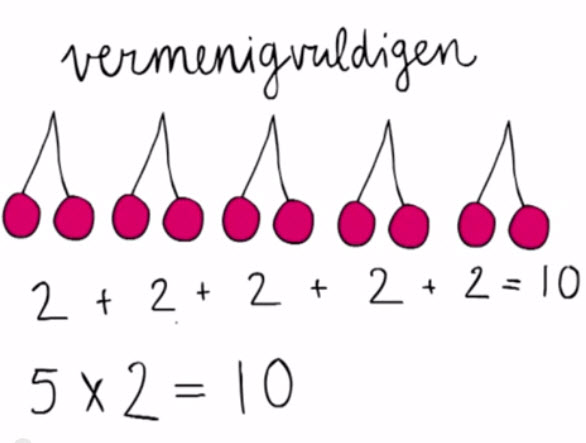Vermenigvuldigen met hele getallen

	1 – Wat is vermenigvuldigen? Voorbeelden van herhaald optellen met groepjes kersen, ijsbolletjes en meer. Uitleg filmpje
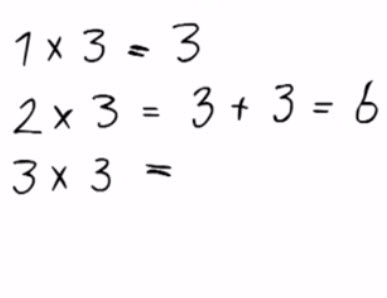	2 – Vermenigvuldigen onder de tien (de tafels van vermenigvuldiging) Uitleg van de tafels. Uitleg filmpje Werkbladen met antwoordbladen
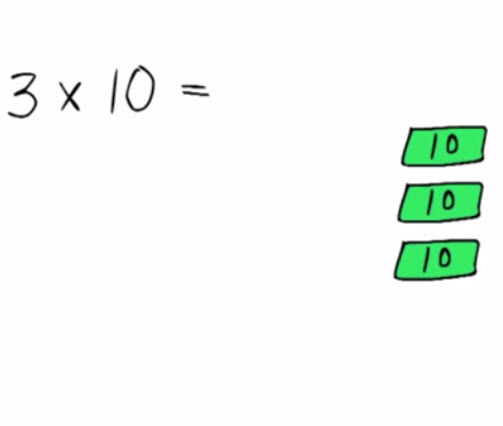	3 – Vermenigvuldigen met 10, 100, 1000, enz. Het is erg belangrijk om meteen te weten hoeveel 3 maal 10 is of 5 maal 1000. Bovendien is het zeer eenvoudig. In de video wordt duidelijk gemaakt waarom ‘maal tien’ niet moeilijker is dan gewoon een nul achter een getal zetten. En dat ‘maal honderd’ twee nullen meer toevoegt achter een getal. Veel oefenen verhoogt het inzicht in het tientallig stelsel. Ook is van belang voor het goed kunnen schatten van de orde van grootte van een antwoord. Uitleg filmpje Werkbladen met antwoordbladen
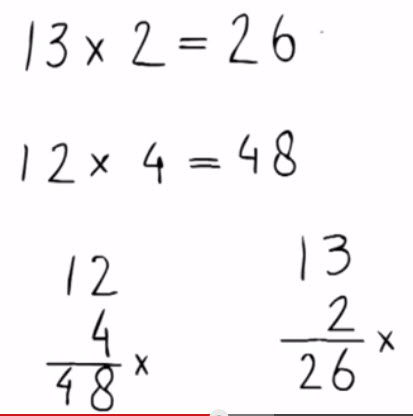	4 – Vermenigvuldigen onder elkaar zonder onthouden Het antwoord op elke vermenigvuldiging kan foutloos en exact worden berekend door de standaardprocedure van het vermenigvuldigen onder elkaar. Het is niet moeilijk om te begrijpen waarom deze methode altijd werkt. Het uitlegfilmpje laat dit zien. Uitleg filmpje Werkbladen met antwoordbladen
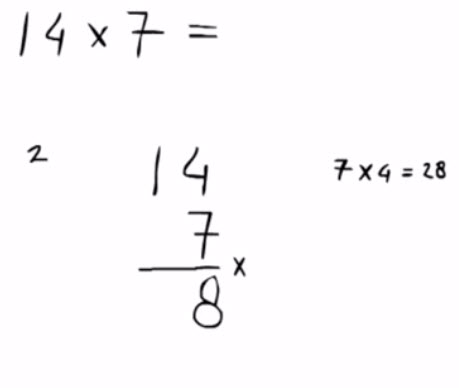	5 – Vermenigvuldigen met onthouden, onder de honderd Vaak krijg je bij het werken onder elkaar een tussen-antwoord van twee cijfers. Je moet dan alleen het tweede cijfer opschrijven en het eerste cijfer even onthouden. Het hoe en waarom wordt in de video uitgelegd. Uitleg filmpje Werkbladen met antwoordbladen
	6 – Vermenigvuldigen met onthouden, met een groot getal Een getal onder de tien maal een getal van drie cijfers of meer, werkt op precies dezelfde manier en is niet moeilijker. Regelmatig wat oefenen maakt dat elke vermenigvuldiging eenvoudig wordt en altijd tot het goede en exacte antwoord leidt. Uitleg filmpje Werkbladen met antwoordbladen
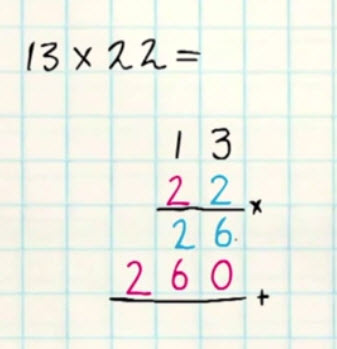	7 – Vermenigvuldigen zonder onthouden van twee getallen boven de tien Bij de vermenigvuldiging van twee grotere getallen zijn meerdere regels nodig maar het is in principe niet echt moeilijker. In het uitlegfilmpje wordt duidelijk gemaakt hoe de standaard procedure werkt en waarom het altijd het goede antwoord geeft. Uitleg filmpje Werkbladen met antwoordbladen
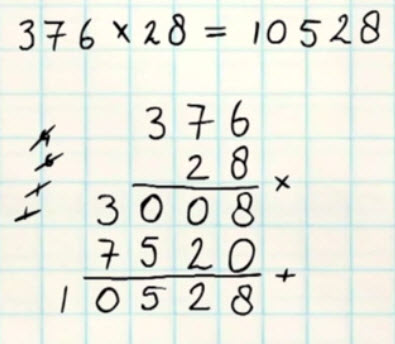	8 – Vermenigvuldigen met onthouden van twee getallen boven de tien Ook bij het product van twee grotere getallen moet je natuurlijk soms even een cijfer ‘onthouden’. Als deze sommetjes met behulp van de werkbladen goed worden geoefend, is geen enkele vermenigvuldiging meer te moeilijk. Elke vermenigvuldiging kan je nu zonder problemen en foutloos uitrekenen! Uitleg filmpje Werkbladen met antwoordbladen

Hier onder de video’s die horen bij de paragrafen over het vermenigvuldigen met hele getallen.
Deze video’s staan ook op de pagina die hoort bij een paragraaf. Ga voor oefenen (online of met werkbladen) naar de paragraaf-pagina.