Hieronder 15 onderdelen over breuken vanaf groep 5. Wat is een breuk?. Hoe schrijf je een breuk op? Hoe groot is een breuk? Breuken oefenen, uitleg en werkbladen en online oefenen.

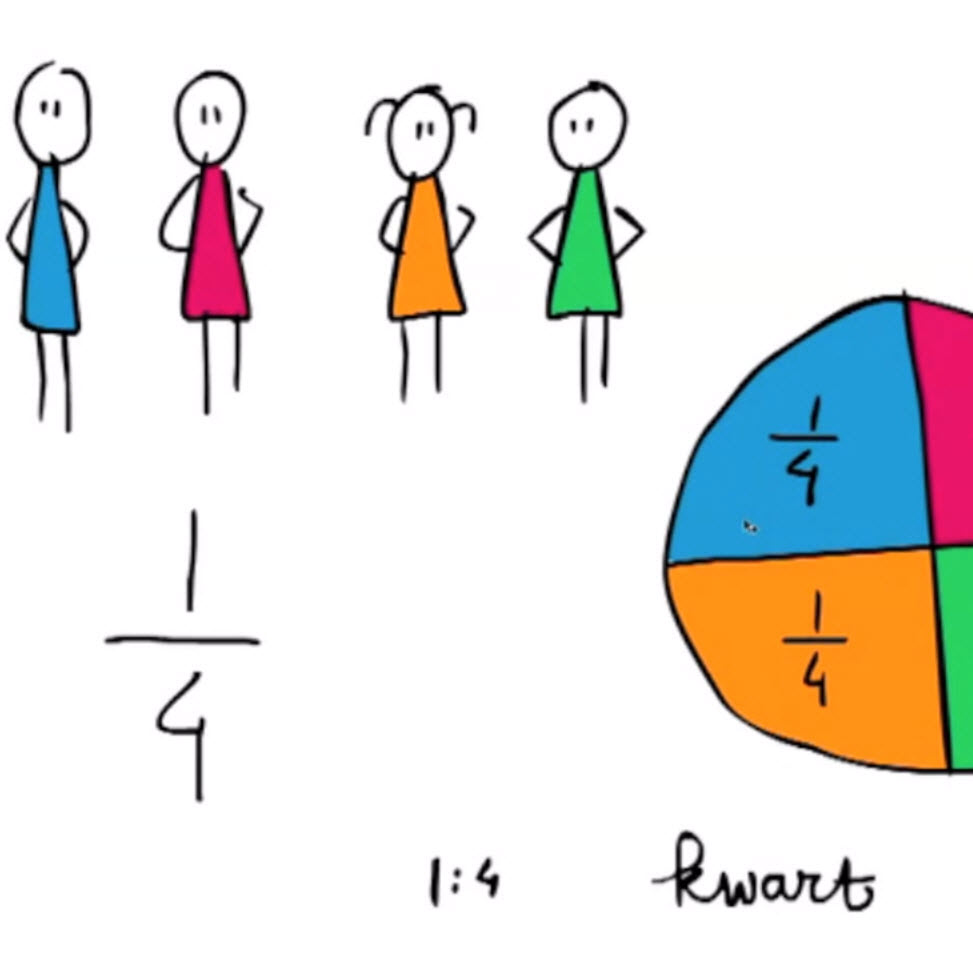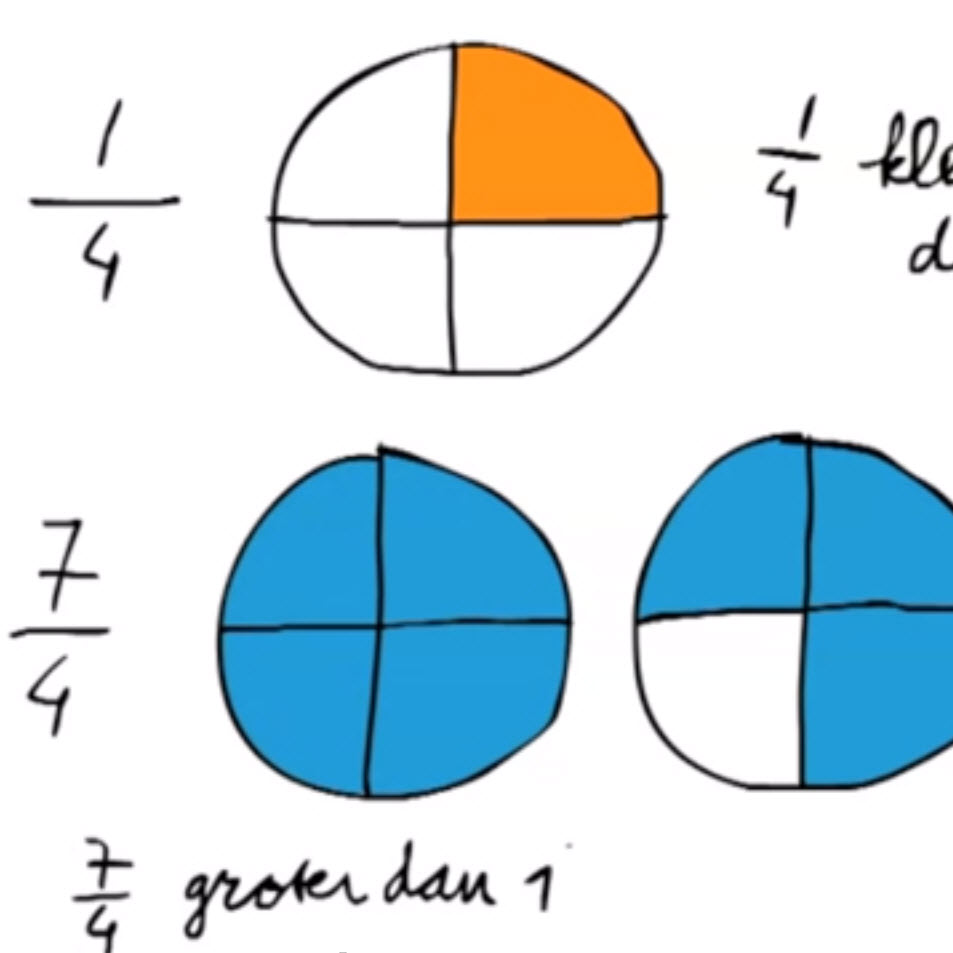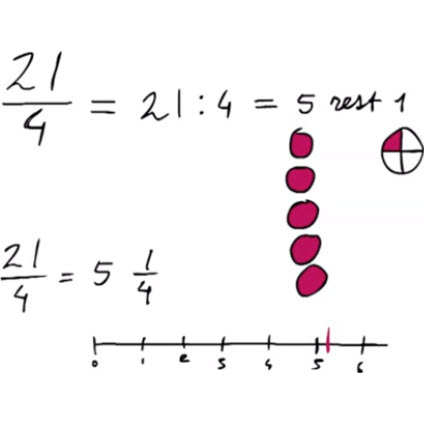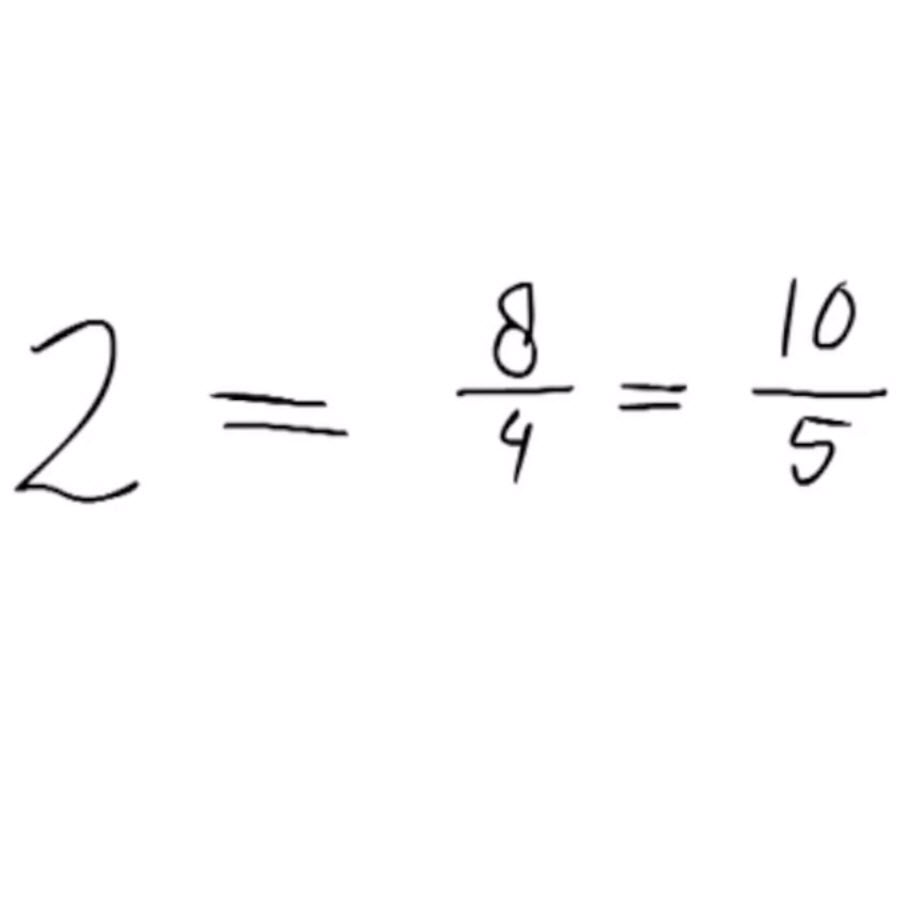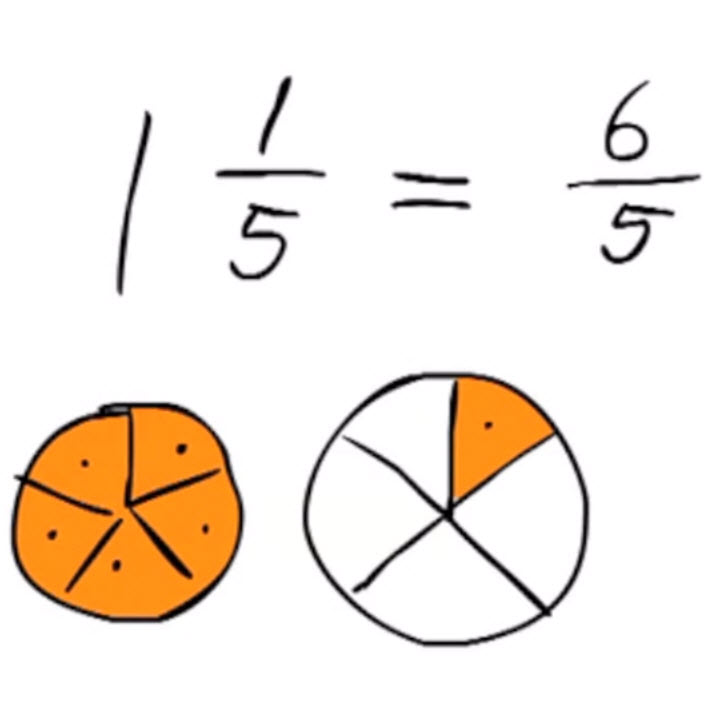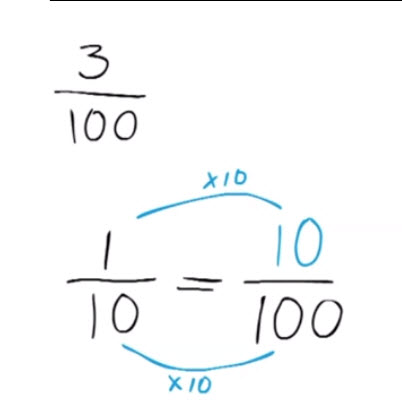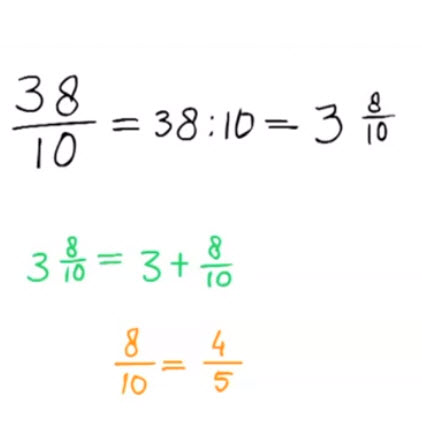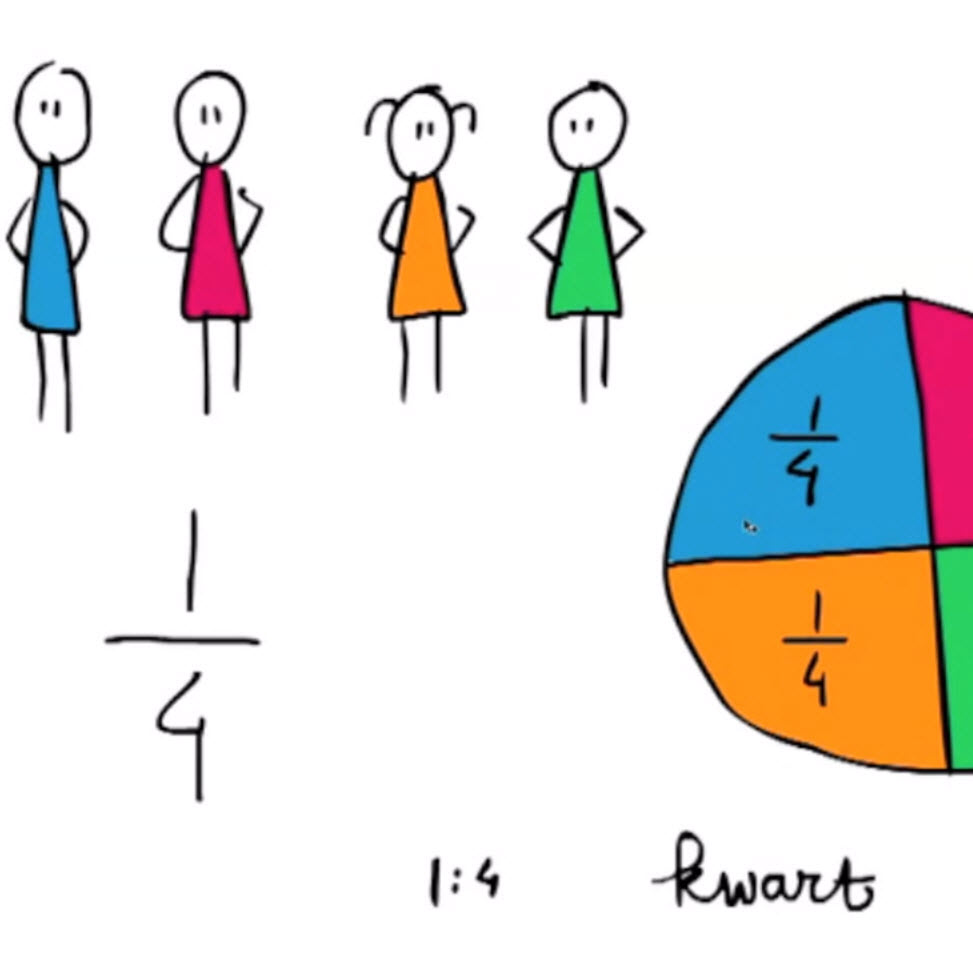
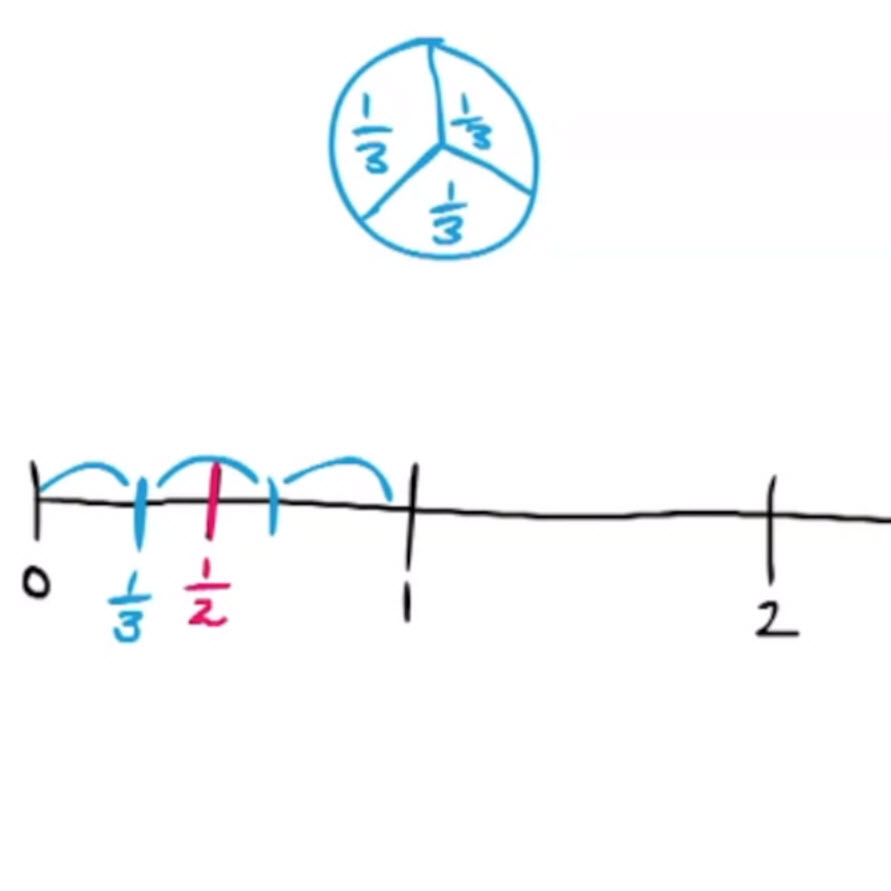
	1 – Een half, een derde en een kwart Breuken, wat zijn dat? Wat betekent een half, een derde of een kwart? Wat is een breukstreep? Uitleg over de breukstreep; een breukstreep is een deelteken. Werkbladen met antwoordbladen over de breuknotatie. Uitleg over een breuk zoals een half of een derde. Online breuken oefenen, het benoemen van een breuk.
	2 – Een breuk op de getallenlijn zetten De breuk 1/2 is een nieuw soort getal. Je kunt deze breuk daarom ook op de getallenlijn zetten. Uitleg over het feit dat een half een nieuw soort getal is. Online breuken oefenen, het plaatsen van een eenvoudige breuk op de getallenlijn.
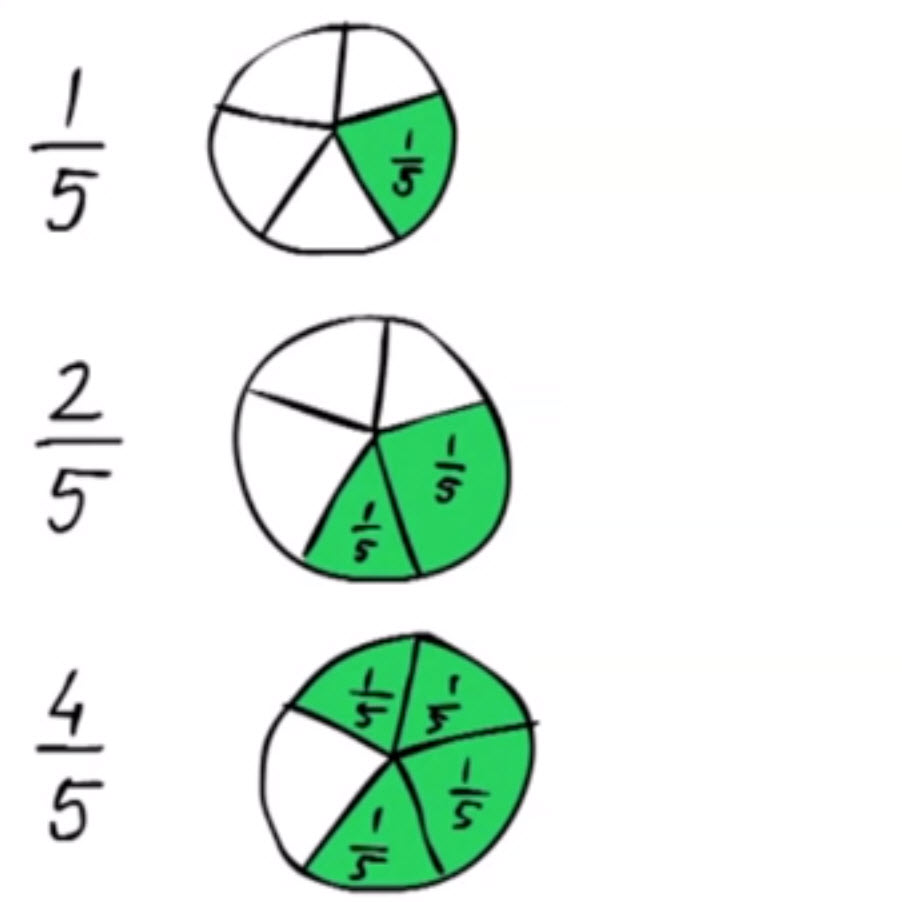
	3 – Twee vijfde De betekenis van 2/5, 3/5, 4/5, 5/5, enz. Uitleg van het feit dat de breuk 3/3 gelijk is aan 1, ook op de getallenlijn. Meer uitleg, ook op de getallenlijn, en het benoemen van een een breuk in pizzamodel. Online breuken oefenen, het plaatsen van een breuk zoals 4/5 op de getallenlijn.
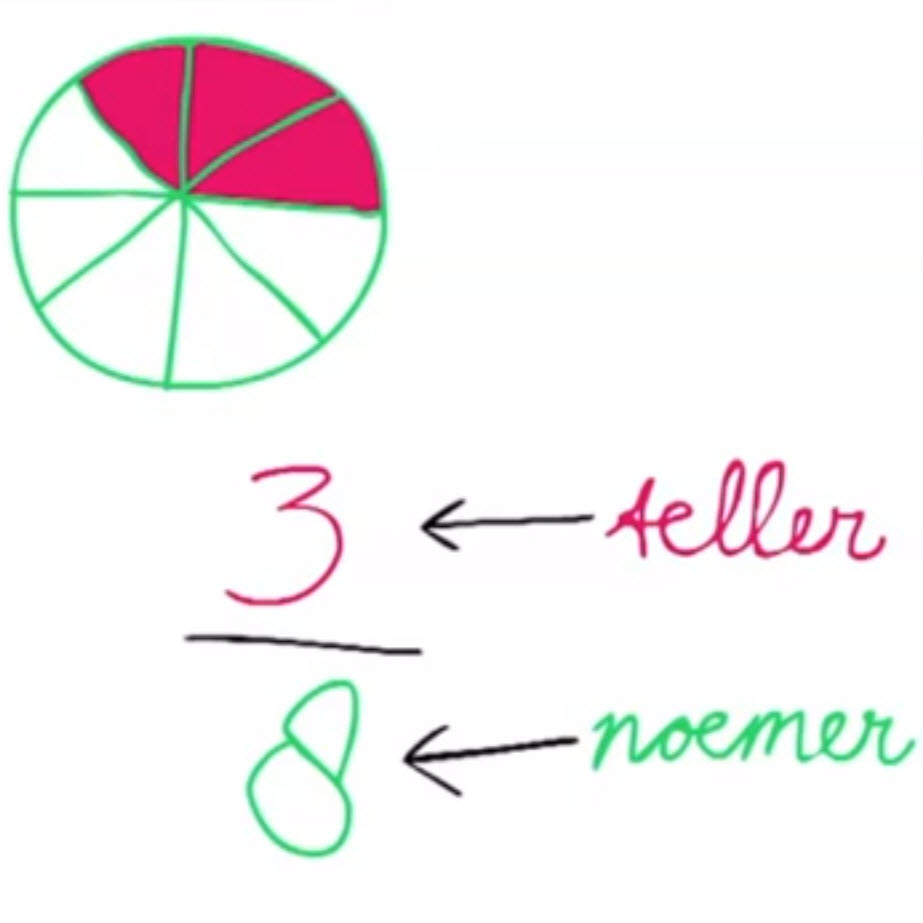
	4 – Teller en noemer De begrippen ’teller’ en ‘noemer’ Uitleg van de woorden ’teller’ en ‘noemer’. Online breuken oefenen, het aangeven van de teller en noemer van een breuk.
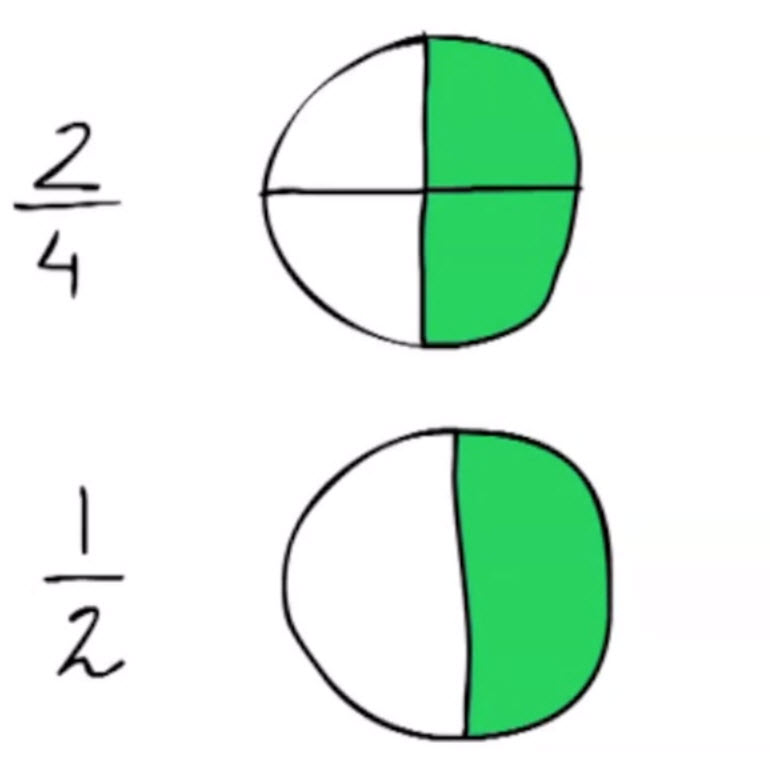
	5 – Een breuk anders opschrijven  Het vereenvoudigen van een breuk Uitleg. Met behulp van tekeningen wordt duidelijk gemaakt dat een breuk dezelfde waarde houdt als je de teller en de noemer van die breuk allebei door hetzelfde getal deelt. Tweede uitleg video waarin wordt uitgelegd waarom je een breuk altijd op oneindig veel manieren kunt opschrijven. Ook wordt dan duidelijk waarom je een breuk meestal zo eenvoudig mogelijk wilt opschrijven. Werkbladen met uitgewerkte antwoordbladen, vereenvoudigen van een breuk. Online breuken oefenen, het vereenvoudigen van een breuk door de teller en de noemer van die breuk te delen door een gemeenschappelijke factor.
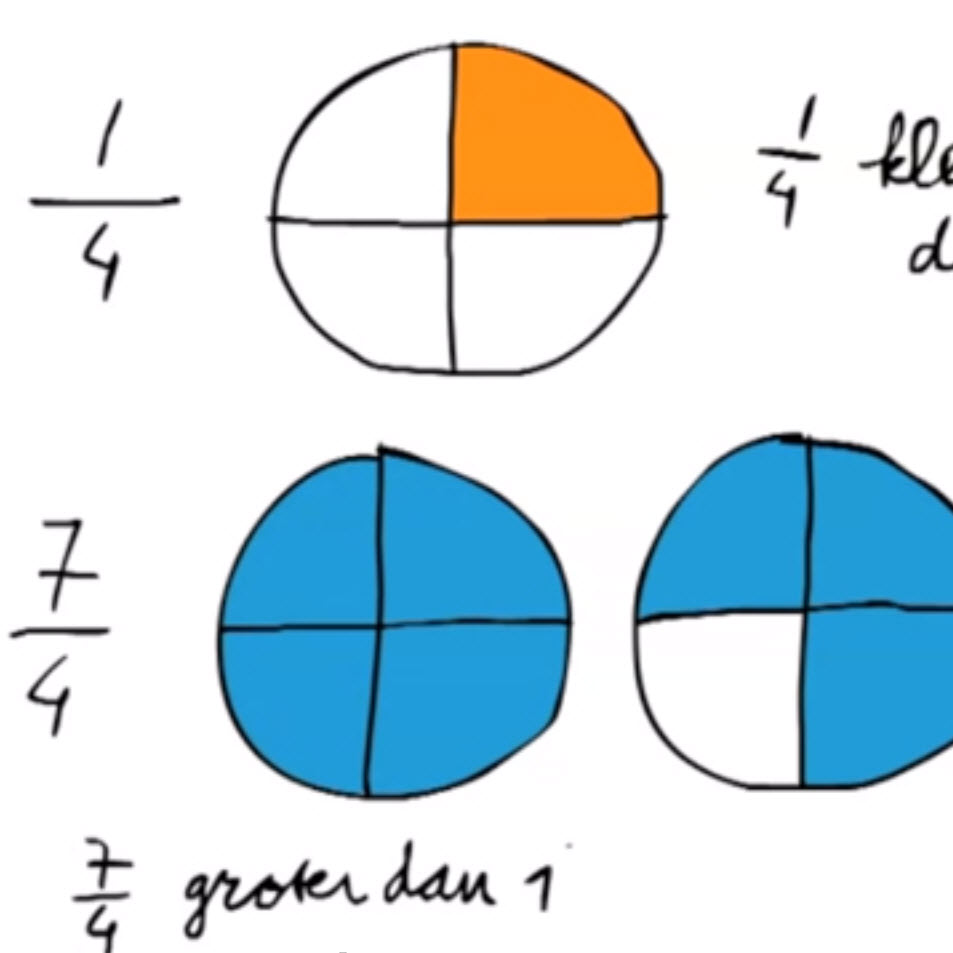
	6 – Gemengde breuken De betekenis van 1 3/4  Uitleg over de betekenis van een gemengde breuk zoals 1 3/4. In de video wordt duidelijk gemaakt waarom je een breuk met teller groter dan noemer soms liever als een gemengde breuk opschrijft. Twee oefenbladen met uitgewerkte antwoordbladen.
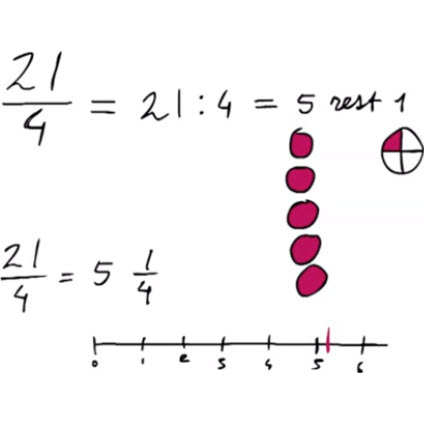
	7 – Een onechte breuk schrijven als een gemengde breuk Een onechte breuk omzetten naar een gemengde breuk Uitleg video. Als de teller van een breuk groter is dan de noemer, is de breuk een deelsom met antwoord groter dan één. Je kunt de uitkomst van de deelsom opschrijven als een heel getal plus nog een breuk. Werkbladen met antwoordbladen. Van onechte breuk naar gemengde breuk. Oefenen op de computer met het op de getallenlijn plaatsen van een onechte of echte breuk.
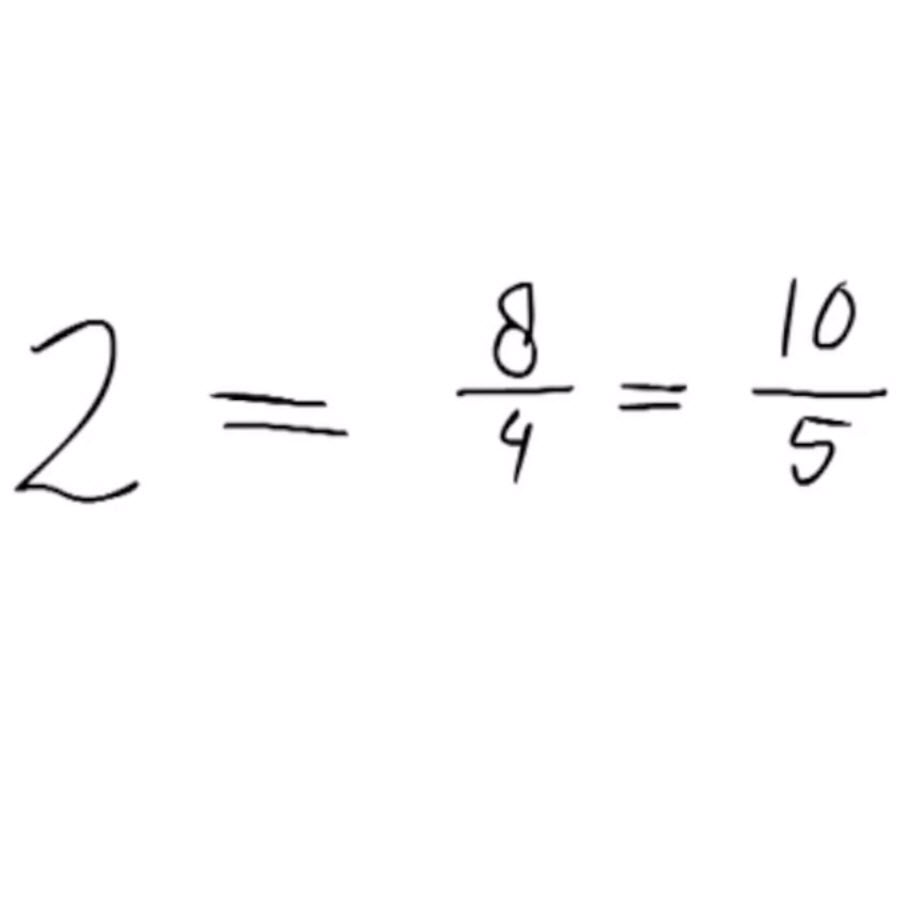
	8 – Een heel getal schrijven als een breuk Een heel getal is het antwoord van oneindig veel deelsommen Uitleg video. Een heel getal is ook altijd het antwoord van een deelsom. Het getal 3 is bijvoorbeeld gelijk aan 3:1 maar het is ook gelijk aan 6:2. Werkbladen met antwoordbladen. Samenvatting van heel getal naar breuk
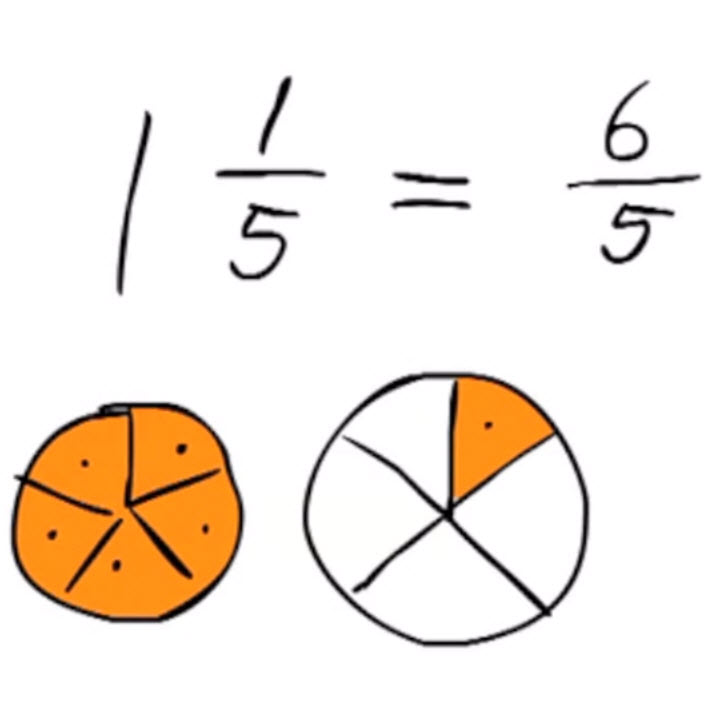
	9 – Van gemengde breuk naar breuk Een heel getal plus een breuk kun je ook altijd opschrijven als een breuk met een teller die groter is dan de noemer Uitleg video. Werkbladen met antwoordbladen. Oefenen op de computer. Je ziet steeds een gemengde breuk. Deze gemengde breuk moet worden omgezet in een breuk met alleen een teller en een noemer. De stap voor stap uitleg wordt ondersteund met gekleurde pizza modellen.
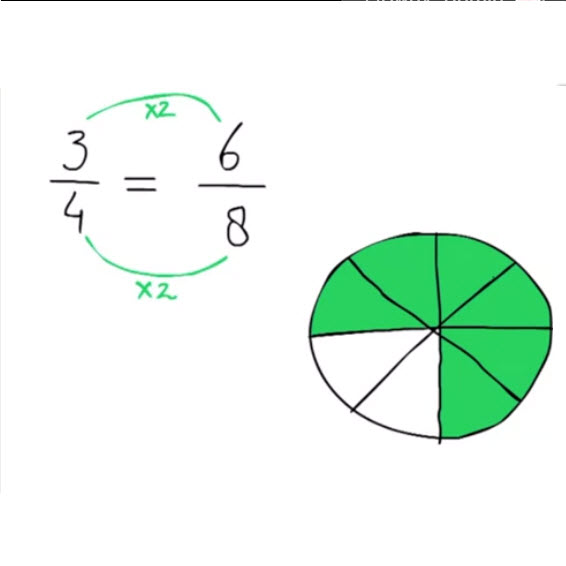
	10 – De noemer groter maken Hoe maak je de noemer van een breuk groter? Uitleg video. Werkbladen met antwoordbladen. Oefenen op de computer. Je wilt bijvoorbeeld 1/6 opschrijven als een breuk met noemer 24. De uitgebreide stap voor stap uitleg wordt verduidelijkt met gekleurde pizza modellen.
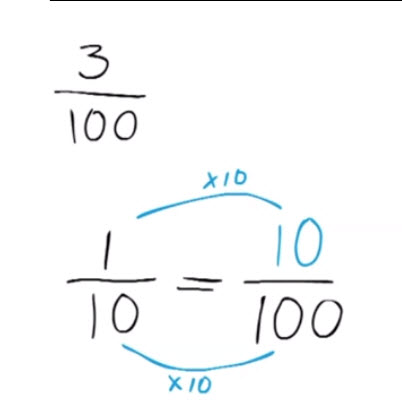
	11 – Twee breuken dezelfde noemer geven Breuken gelijknamig maken Uitleg video. Waarom wil je twee breuken soms gelijknamig maken en hoe doe je dat? Werkbladen met uitgewerkte antwoordbladen. Oefenen op de computer met het groter en kleiner dan teken tussen twee gelijknamige breuken. Oefenen op de computer met het gelijknamig maken van twee breuken en vervolgens bepalen welk van de twee breuken de grootste is.
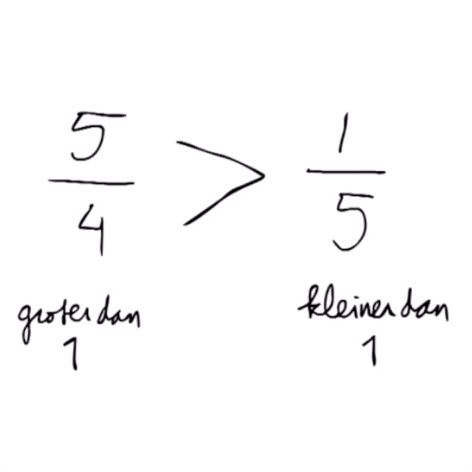
	12 – Welke breuk is groter, 1/3 of 1/5 ? (tellers 1) Het vergelijken van twee breuken met teller 1 Uitleg video. Werkbladen met antwoordbladen. Kies steeds tussen het kleiner-dan-symbool of het groter-dan-symbool. Oefenen op de computer. Uitleg wordt ook steeds visueel gemaakt met pizza model.
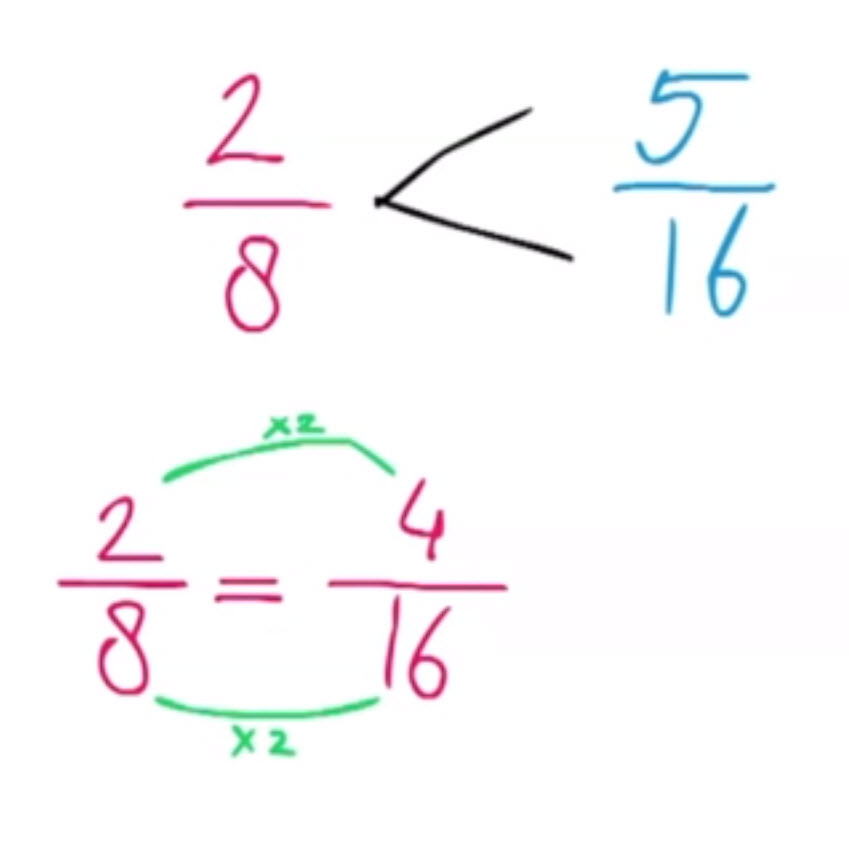
	13 – Welke breuk is groter, 4/3 of 5/8 ( een onechte breuk en een echte breuk) ? Bij het vergelijken van twee breuken bekijk je een breuk altijd eerst als een deelsom. Uitleg video. Je bekijkt elke breuk eerst als een deelsom. Soms is het antwoord van een van beide deelsommen groter dan 1. Je ziet dan in een oogopslag welke breuk groter is. Werkbladen met antwoordbladen. Te gebruiken als oefening maar ook goed te gebruiken als toets. Oefenen op de computer met het invullen van het groter-dan teken of het kleiner-dan teken tussen twee breuken waarvan een van beide een waarde heeft die groter is dan 1. Bij elke vraag ook hints met uitleg.
	14 – Welke breuk is groter, 2/8 of 5/16? Het vergelijken van twee willekeurige breuken d.m.v. gelijknamig maken  Uitleg video. Soms moet je eerst de noemers gelijk maken voordat je kunt zien welke breuk de grootste is. Werkbladen met uitgewerkte antwoordbladen. Oefenen op de computer. De breuken worden in de hints eerste gelijknamig gemaakt door de teller en noemer van een breuk met een zelfde factor te vermenigvuldigen.
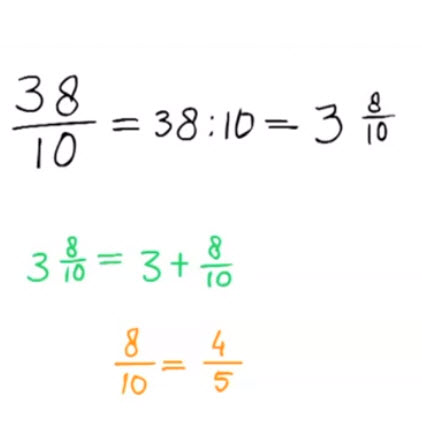
	15 – Een breuk vereenvoudigen Een onechte of echte breuk zo eenvoudig mogelijk opschrijven Uitleg video. Bekijk de breuk eerst als deelsom. Daarna kijken of de teller en de noemer een gemeenschappelijke factor hebben. Werkbladen met uitgewerkte antwoordbladen. Oefenen op de computer. Ook in deze oefening bekijk je de breuk eerst als deelsom. Daarna wordt gekeken of de teller en de noemer allebei door een zelfde getal gedeeld kunnen worden.

Hier onder de eerste video’s die horen bij de paragrafen over Inleiding Breuken.
Deze video’s staan ook op de pagina die hoort bij een paragraaf. Ga voor oefenen (online of met werkbladen) naar de paragraaf-pagina.